The elusive Wigner Crystal as a condensation in the space of quantum states
Phase transitions are ubiquitous and their study is crucial for our understanding of the different states of matter and their relationships. Common examples include gas-liquid and solid-liquid transitions, achievable by smoothly changing one external parameter like the temperature. If the system has predominant quantum features, phase transitions are possible also at zero temperature. Quantum phase transitions (QPTs) are characterized by a competition between two qualitatively different ground states reachable by varying one external parameter of the Hamiltonian of the system. When this external parameter smoothly runs through a critical value, in the thermodynamic limit, an order parameter of the system experiences an abrupt change.
The above scenario becomes much more intriguing if the constituents of the system are electrons. In 1934 Eugene Wigner predicted that, despite their strong coulomb repulsion, under suitable conditions, electrons could form a crystal! Wigner did not use statistical mechanics arguments, he just compared the kinetic energy of an electron gas with the Coulomb repulsion energy and noticed that, when the latter dominates, i.e., at low densities, electrons may find energetically more convenient to distribute regularly through the hosting metal.
The phenomenon is extremely complex: the mentioned energetic balance does not imply that electrons get frozen as in an ordinary crystal (when brought at zero temperature). On the contrary, the metal can still conduct electric current. Since the 1934 conjecture, no one has been able to establish whether Wigner crystallization is a real QPT or not. In a recent paper, published in Physical Review Letters, Massimo Ostilli and Carlo Presilla have finally proved that Wigner crystallization is a first order QPT: by using quantum statistical mechanics arguments, they show that, under rather mild conditions, by decreasing the density (external parameter) the ground state energy of the electron gas (order parameter) shows a discontinuity in its first order derivative with respect to the density itself.
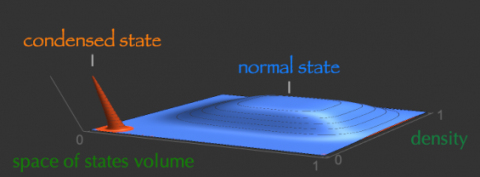
The proof is mathematically rigorous and the authors provide exact upper and lower bounds for the critical density. By demanding Monte Carlo simulations (running for several months in the supercomputing facilities of INFN Sezione di Roma 1 and Cineca) they also give a numerical estimate of the precise critical point. Interestingly, the used mathematical framework shows that the emergent collective behavior which manifests in the thermodynamic limit can be interpreted as a condensation, but not as a condensation of matter in the ordinary space, rather as a condensation of degrees of freedom within the space of states allowed by quantum mechanics. In this way, Wigner's informal argument is replaced by a rigorous picture borrowed from the paradigma of condensation phenomena taking place, however, in the amazing complex space of the quantum wavefunctions.
Authors:
Massimo Ostilli, Carlo Presilla
Reference:
Physical Review Letters
