Hidden transition in multiplex networks
Wednesday Apr 27, 2022, 4:00 PM → 6:00 PM Europe/Rome
Aula Conversi (Dip. di Fisica Edificio G. Marconi)
We report a novel discontinuous phase transition, distinct from a hybrid one, in weak multiplex percolation on networks of three or more layers. Weak multiplex percolation generalizes percolation to multi-layer networks, represented as networks with a common set of vertices linked by multiple types (colours) of edges. In this kind of percolation, every vertex in a giant component has at least one connection in each layer to another vertex in this component.
This definition is local in contrast to the one for a giant mutually connected component. Weak multiplex percolation is a particular case of the k-core problem for multiplex networks.
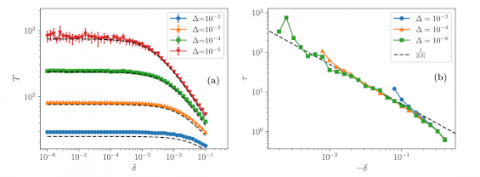
We describe an anomalous discontinuous phase transition in the weak percolation problem occurring in multiplex networks of three or more layers without unconnected vertices, P(0) = 0, where P(q) is the degree distribution for each of the layers. The control parameter for this transition is the fraction of vertices in each layer with a single connection, P(1). In an undamaged network of this kind, the giant component defined as explained above includes all vertices for any value of the control parameter. It turns out that above a critical value of the control parameter the removal of even a tiny fraction of nodes or edges triggers a failure cascade which ends with the total collapse of the network. Below the critical point, this vanishingly small damage has a null effect.
We demonstrate that critical singularities associated with this novel phase transition differ from those for standard hybrid phase transitions. We obtain asymptotic expressions for the collapse time of the giant component to zero and the relaxation time of this component above and below the critical point, respectively. Both these characteristic times show the Curie–Weiss law singularity at the critical point in contrast to the inverse square root singularity for these times for a standard hybrid phase transition.
Link zoom: https://uniroma1.zoom.us/j/82330282429?pwd=MktKdmlkSUxxdXlraFhKSHhJTDZnUT09
